
Détection d'orientation IoT par IMU
Système IoT pour détecter l'état d'emballages pliables via capteurs inertiels et transmission LPWAN optimisée.
Le défi de la logistique intelligente
Un client spécialisé dans la logistique industrielle utilisait des caisses en bois pliables pour optimiser le transport et le stockage de marchandises. Ces emballages intelligents peuvent prendre trois configurations distinctes :
- Fermée : prête pour le transport
- Ouverte : en cours d'utilisation
- Pliée : optimisation de l'espace de stockage
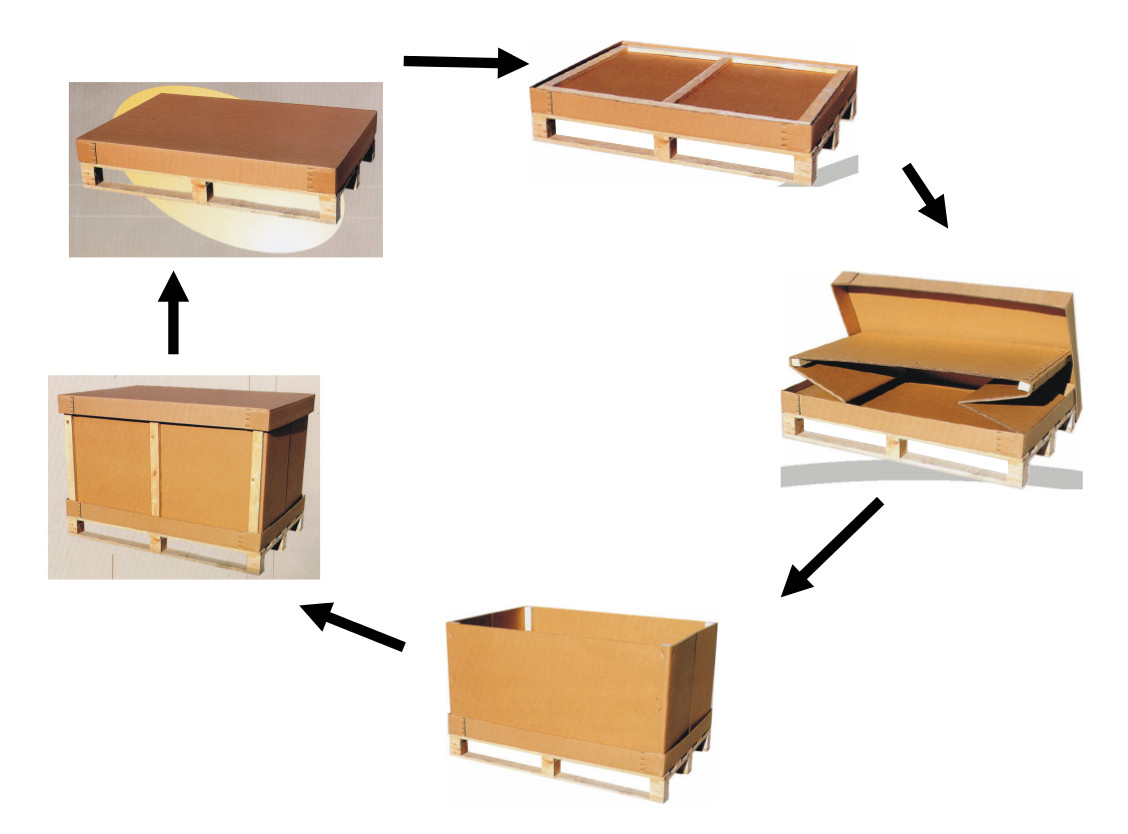
L'objectif était de développer un système IoT capable de détecter automatiquement l'état de chaque caisse et de transmettre cette information via un réseau LPWAN (Sigfox) avec une consommation énergétique minimale.
Principe de détection par orientation
La solution repose sur un principe élégant : en fixant un capteur inertiel (IMU) sur le couvercle de la caisse, il devient possible de détecter l'état uniquement en mesurant l'orientation du capteur dans l'espace.

Cette approche présente plusieurs avantages techniques majeurs :
- Simplicité du capteur : Un simple accéléromètre 3 axes suffit
- Robustesse : Pas de pièces mécaniques mobiles
- Faible consommation : Transmissions ponctuelles uniquement
Optimisation de la transmission LPWAN
Un défi majeur était l'optimisation de la bande passante pour les réseaux LPWAN comme Sigfox, qui sont limités en débit et en nombre de messages quotidiens. Avec trois états possibles plus un état d'erreur, l'encodage optimal nécessite seulement 2 bits :
| Code binaire | État détecté |
|---|---|
| 00 | Fermé |
| 01 | Ouvert |
| 10 | Plié |
| 11 | État inconnu / Erreur |
Mesure et analyse du vecteur gravité
Le principe de détection repose sur l'analyse du vecteur gravité mesuré par l'accéléromètre. Dans chaque configuration, ce vecteur pointe vers le centre de la Terre mais son orientation relative dans le repère du capteur change selon l'état de la caisse.
Pour mesurer l'orientation, il suffit de mesurer le vecteur gravité qui est différent dans les trois positions. Un accéléromètre au repos ne mesure que l'accélération due à la gravité terrestre (environ 9,81 m/s²), qui constitue une référence d'orientation absolue parfaite.

En deux dimensions, l'exemple serait assez simple à résoudre, mais en réalité nous travaillons avec trois axes et nous pouvons être amenés à identifier des orientations dans toutes les directions de l'espace. Cette complexité tridimensionnelle nécessite une approche algorithmique robuste basée sur l'algèbre vectorielle.
Algorithme de reconnaissance d'orientation
L'algorithme développé suit une approche en plusieurs étapes pour identifier de manière robuste l'orientation du capteur :
1. Mesure expérimentale des vecteurs de référence
La première étape consiste à déterminer expérimentalement un vecteur gravité pour chaque orientation possible de la caisse. Pour cela, on place physiquement la caisse dans chacune des trois configurations (fermée, ouverte, pliée) et on enregistre les mesures de l'accéléromètre.
Ces mesures sont ensuite normalisées pour obtenir des vecteurs unitaires qui serviront de références. Cette calibration empirique garantit que l'algorithme s'adapte aux conditions réelles d'installation du capteur.
2. Définition des structures de données
Une fois les vecteurs de référence déterminés, nous définons les structures nécessaires pour représenter les vecteurs 3D et les états d'orientation :
// Structure pour représenter un vecteur 3D
typedef struct {
float x; // Composante X (axe avant/arrière)
float y; // Composante Y (axe gauche/droite)
float z; // Composante Z (axe haut/bas)
} Vector3D_t;
// Vecteurs de référence pour chaque orientation (normalisés)
// Ces valeurs sont mesurées expérimentalement lors de la phase de calibration
// en plaçant physiquement la caisse dans chaque configuration
Vector3D_t orientationVectors[] = {
{0.0f, 0.0f, -1.0f}, // Fermé : gravité vers le bas du capteur
{0.9f, 0.0f, 0.44f}, // Ouvert : capteur incliné ~26° (mesuré)
{0.31f, 0.0f, 0.95f}, // Plié : capteur incliné ~72° (mesuré)
};
// Nombre de vecteurs de référence définis
const int n_vectors = sizeof(orientationVectors) / sizeof(orientationVectors[0]);
// Énumération des états possibles
typedef enum {
CLOSED = 0b00, // Caisse fermée
OPEN = 0b01, // Caisse ouverte
FOLDED = 0b10, // Caisse pliée
UNKNOWN = 0b11 // État indéterminé
} Orientation_t;3. Mathématiques du produit scalaire
La reconnaissance d'orientation utilise le produit scalaire entre le vecteur gravité mesuré et les vecteurs de référence. Cette approche exploite une propriété fondamentale de l'algèbre vectorielle :
\[\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos(\theta)\]
Où θ est l'angle entre les deux vecteurs
Comme nos vecteurs sont normalisés (norme = 1), le produit scalaire nous donne directement cos(θ), permettant une mesure simple et efficace de l'angle entre les orientations.
4. Implémentation de l'algorithme
L'algorithme final combine normalisation vectorielle et comparaison par produit scalaire avec seuillage adaptatif :
// Configuration du seuil de tolérance angulaire
#define MAX_ANGLE_DEGREES 10.0f // Tolérance maximale en degrés
#define DEG_TO_RAD (3.14159265f / 180.0f) // Conversion degrés -> radians
// Calcul du seuil : cos(angle_max)
// Plus l'angle autorisé est petit, plus le seuil est proche de 1
const float threshold = cos(MAX_ANGLE_DEGREES * DEG_TO_RAD);
/**
* Détermine l'orientation de la caisse à partir du vecteur gravité mesuré
*
* @param gravity Vecteur gravité brut de l'accéléromètre
* @return État détecté (CLOSED, OPEN, FOLDED, ou UNKNOWN)
*/
Orientation_t getOrientation(Vector3D_t gravity) {
// Étape 1: Normalisation du vecteur gravité mesuré
float norm = sqrt(gravity.x * gravity.x +
gravity.y * gravity.y +
gravity.z * gravity.z);
// Vérification de la validité de la mesure
if (norm == 0.0f) {
return UNKNOWN; // Évite la division par zéro
}
// Création du vecteur normalisé
Vector3D_t normGravity = {
gravity.x / norm,
gravity.y / norm,
gravity.z / norm
};
// Étape 2: Comparaison avec chaque vecteur de référence
for (int i = 0; i < n_vectors; i++) {
// Calcul du produit scalaire = cos(θ)
float dotProduct = normGravity.x * orientationVectors[i].x +
normGravity.y * orientationVectors[i].y +
normGravity.z * orientationVectors[i].z;
// Si l'angle est suffisamment petit (cos(θ) > threshold)
if (dotProduct > threshold) {
return (Orientation_t)i; // Orientation reconnue
}
}
// Aucune orientation reconnue avec la tolérance définie
return UNKNOWN;
}Avantages et inconvénients de la solution
Cette approche basée sur l'algèbre vectorielle présente plusieurs avantages significatifs :
- Simplicité algorithmique : Opérations arithmétiques légères, parfaitement adaptées aux microcontrôleurs basse consommation
- Pas d'apprentissage requis : Algorithme déterministe sans phase d'entraînement, calibration directe par mesure physique
- Transmission ultra-optimisée : Seulement 2 bits par message sur les réseaux LPWAN contraints
- Configuration simplifiée : Seulement un seuil angulaire en degrés à configurer pour la sensibilité
- Compatible avec calibration automatique : Cette solution se combine parfaitement avec les méthodes de calibration automatique d'IMU si l'orientation de fixation de l'équipement n'est pas connue précisément
Le principe développé est facilement extensible à d'autres cas d'usage comme par exemple la détection d'un changement d'orientation sans nécessairement identifier d'orientations prédéfinies pour détecter une chute, un mouvement anormal, etc.
Démonstration interactive : Détection d'orientation par IMU
Simulation interactive de la détection d'orientation d'un capteur IMU. Vous pouvez ajuster l'angle du capteur et voir en temps réel comment l'algorithme détecte les orientations de référence configurées.
Expérience optimale sur ordinateur
Cette démonstration interactive est conçue pour être
utilisée sur un écran d'ordinateur avec une souris ou
un trackpad.
Les interactions tactiles peuvent ne pas fonctionner correctement sur cette démonstration.
Un projet IoT similaire vous intéresse ?
Discutons de vos besoins en instrumentation IoT et capteurs intelligents.